Simple Compass Oscillations

Jalves S. Figueira, Federal Technological University of Paraná, PR, Brazil

The proportionality constant ß depends on the properties of the system and determines the speed with which the energy is transferred to the neighborhood, reducing the amplitude of the oscillations and leading the system to rest.

Our interest is to describe those very private systems, with total mechanical energy proportional to the square of the amplitude, called damped harmonic oscillations. We can rewrite Eq. (1) in function of the displacement

With

corresponding to the angular position at t=0 and

to the damping constant. Finally, getting the function that describes the damped harmonic movement,

with angular frequency

is the initial phase and

to the damping constant. The eq. (3) was obtained from a very particular analysis, however this is the general solution of the linear second order ordinary differential equation.

The objective of this experimental activity is to determine the damped amplitudes of three compasses immersed in various fluids (Fig.2). The used compasses are of common use, without the need for any physical change in the magnetic needle. Give preference to those compasses whose needle tips have all extension of a single color (Fig.1). This feature makes it easy to use the Auto Tracker tool.

Fig. 1 - One of the needle tips has all the extension in red which facilitates the use of Auto Tracker.

Fig.2 - Measurements of angular displacement versus time for compasses immersed in air(red), water(black) and oil(blue).

Which is the best Damping Coefficient for a Compass? Jalves S. Figueira, Federal Technological University of Paraná, PR, Brazil

In certain practical problems we have an interest that the oscillations of a mechanical system are damped as soon as possible. On the vibrations of a car when going through irregular floors, the shock absorbers have the function of dissipating the mechanical energy in a short period of time. This time is crucial for the well-being of passengers and for the good performance of the vehicle. In the same way, the vibrations of the magnetic needle around the North-South direction are undesirable for those looking for finding a certain direction. The oscillations of a magnetic needle energy is dissipated by two processes. The first is result from torques produced by contact forces between the needle and the support pin. This resistive force is approximately constant and depends on the nature of the materials and the degree of surface polishing. The second cause of energy dissipation is the resistance that the fluid provides to the displacement, for low speeds the resistance depends on the viscosity of the fluid being proportional to the speed, . In the latter case, in which the torques are proportional to speed, the dissipation of mechanical energy obeys to a very simple law of proportionality.
		(1)
The proportionality constant ß depends on the properties of the system and determines the speed with which the energy is transferred to the neighborhood, reducing the amplitude of the oscillations and leading the system to rest.
Exponential Decay
Our interest is to describe those very private systems, with total mechanical energy proportional to the square of the amplitude, called damped harmonic oscillations. We can rewrite Eq. (1) in function of the displacement .
	(2)
With corresponding to the angular position at t=0 and to the damping constant. Finally, getting the function that describes the damped harmonic movement,
	(3)
with angular frequency , is the initial phase and to the damping constant. The eq. (3) was obtained from a very particular analysis, however this is the general solution of the linear second order ordinary differential equation.
Tracker Video Experiment
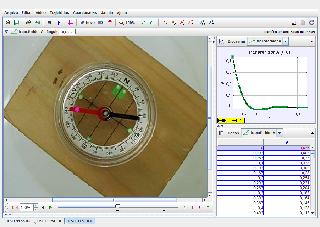
The objective of this experimental activity is to determine the damped amplitudes of three compasses immersed in various fluids (Fig.2). The used compasses are of common use, without the need for any physical change in the magnetic needle. Give preference to those compasses whose needle tips have all extension of a single color (Fig.1). This feature makes it easy to use the Auto Tracker tool.
Fig. 1 - One of the needle tips has all the extension in red which facilitates the use of Auto Tracker.

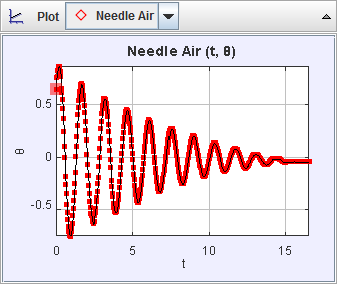
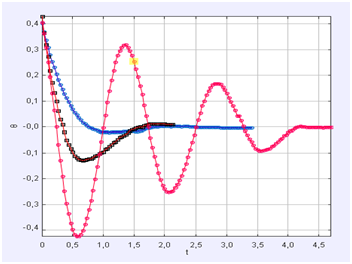
On the first video the magnetic needle is immersed in air (A), the other uses oil (0) for the damping fluid. And a last one changed with water (W). Donwload Experiment Tracker.Zip. From the film analysis using the Tracker tool, please try to answer the following questions: 1. After obtaining the graphics displacement versus time (Fig. 2), determine the period of oscillations. Are all curves periodic system? See that the curve (blue) in which the system does not pass at all through the equilibrium position is called critical damping. 2. Why should we choose small angles to a harmonic oscillator? 3. If the displacement, air compass (red line in Fig.2) variation is sinusoidal how would you describe the speed and acceleration variations? 4. After determining estimate the period of the oscillation, use the Data Tool for estimate the damping constant for water (black), air (red) and oil (blue). Which model best describes immersed in air compass? Linear or exponential function, why? 5. What is the effect of moment inertia and Earth magnetic field for determine the damping constant? Compare with the model of a damped pendulum. 6. We suggest that this experiment be made with liquids of different values of viscosity in order to compare the damping constants in each case, as a relative measurement of the viscosity of these media. 7. What is the best value for the decay of a compass?

Fig.2 - Measurements of angular displacement versus time for compasses immersed in air(red), water(black) and oil(blue).
Tracker.Zip Download Video Water, Video Oil and Video Air References B. Lunkm and R. Beichner. "Exploring Magnetic Fields with the Compass" . Phys. Teach. 49 – 45-48 (Jan. 2011). R. Feynman, B. Robert, Leighton and M. Sands . “The Feynman Lectures on Physics”, Vol. I.

Which is the best Damping Coefficient for a Compass?

Exponential Decay

Tracker Video Experiment

References